En este caso, el coeficiente principal es 1; el coeficiente lineal es par y asume la forma :

x² + 2mx + n = 0

cuyas raíces son

-m ( + – ) √ m² – n

En este caso aparece como coeficiente del término de primer grado un número par 2m y la ecuación es :

ax² + 2mx + n = 0

cuyas raíces son:
-m ( + – ) √ m² – n

Es una ecuación de la forma ax^2m+bx^m+c=0 , donde usualmente a, b y c son números racionales; a ≠ 0 y m es un número entero no menor de 2.

Para resolver se hace la sustitución x^m= t, con lo que resulta la ecuación original como at²+bt+c=0.

Finalmente de x^m= t se hallan los valores de x mediante x=t^1/m; con seguridad, en el campo de los números complejos, hay 2m raíces.

EJEMPLO

La ecuación x⁶+x³+1= 0 , la que se obtiene al factorizar la ecuación binomia de noveno grado: x⁹-1= como diferencia de cubos.

Haciendo el reemplazo x³=t, resulta t²+t+1=0, cuyas raíces son precisamente las raíces cúbicas de la unidad: 1, ω, ω². Las sendas raíces cuadradas de estos números complejos son las seis raíces de la ecuación.

Sin término independiente

Son de la forma:

ax² + bx = 0, cuyas raíces son x₁ = 0;  x₂ = -b/a

Sin término lineal

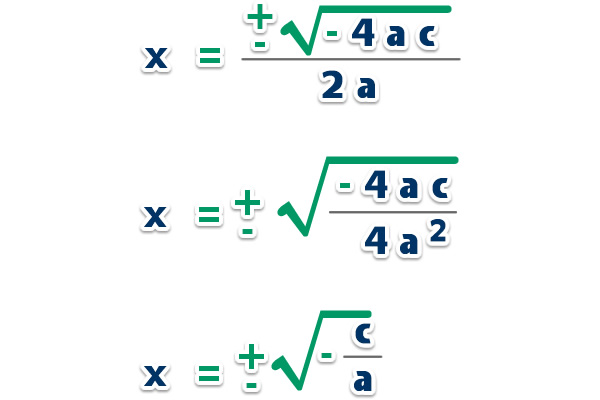
Son de la forma ax² + c = 0 , cuyas raíces son reales opuestos o imaginarios puros opuestos:

Si -c/a > 0 las raíces son reales:

x1 : ax2 = -c o x2 : ax2 = c

Si -c/a < 0 las raíces son imaginarias puras:

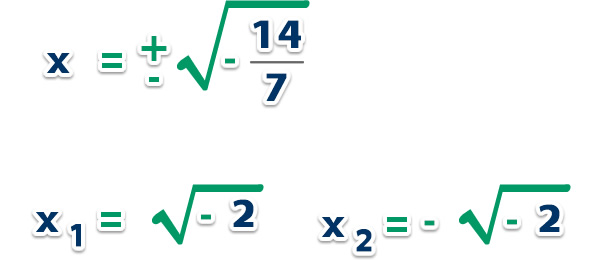
Una ecuación de segundo grado o ecuación cuadrática de una variable es una ecuación que tiene la expresión general:

Ecuación de segundo grado

ax² + bx + c = 0       a ≠ 0

donde x es la variable, y a, b y c constantes; a es el coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede interpretar mediante la gráfica de una función cuadrática, es decir, por una parábola.

• 

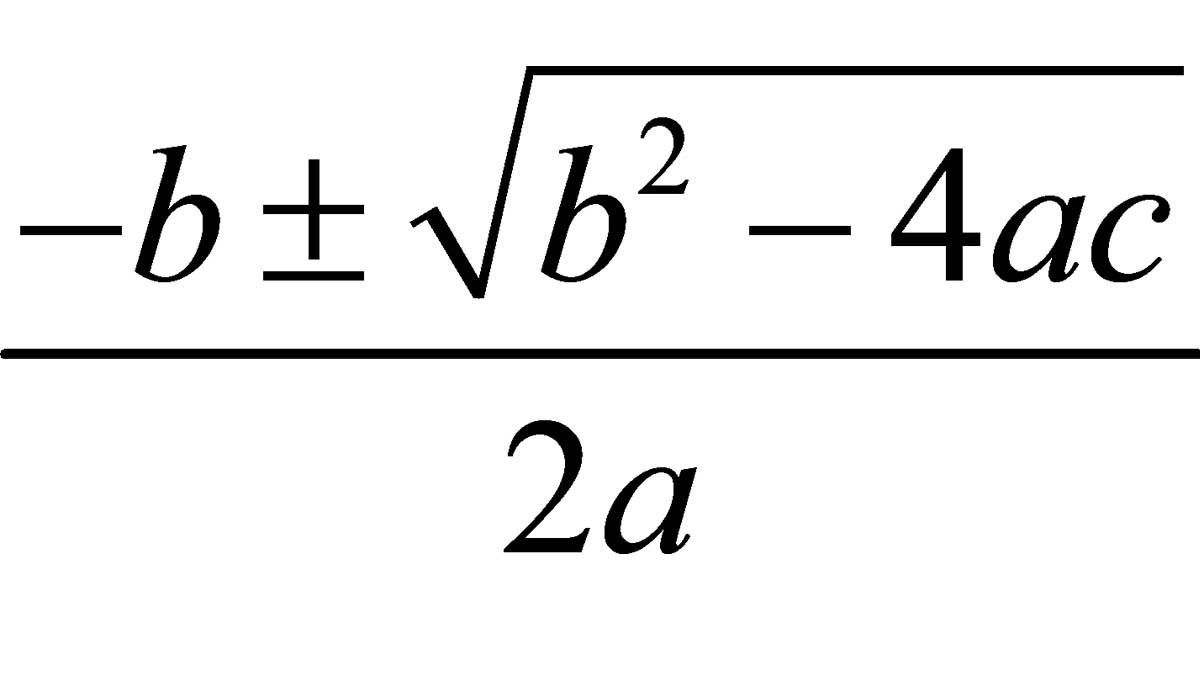
Ecuaciones incompletas

Sin término independiente:

Son de la forma: 

ax² + bx = 0, cuyas raíces son x¹= 0;   x2=-b/a.

Ecuaciones bicuadradas

Éstas son un caso particular de la ecuación de cuarto grado. Les faltan los términos a la tercera y a la primera potencias. Su forma polinómica es:

ax⁴ + bx2 + c = 0

Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable x² = u
Con lo que queda: au² + bu + c = 0. El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula anterior con x¹ y x².

Al deshacer el cambio de variable aparecen las cuatro soluciones:

• X1 = + √u1
• X2 = – √u1
• X3 = + √u2
• X4 = – √u2