Una ecuación de segundo grado o ecuación cuadrática de una variable es una ecuación que tiene la expresión general:
Ecuación de segundo grado
ax2 + bx + c = 0 a ≠ 0
donde x es la variable, y a, b y c constantes; a es el coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede interpretar mediante la gráfica de una función cuadrática, es decir, por una parábola.
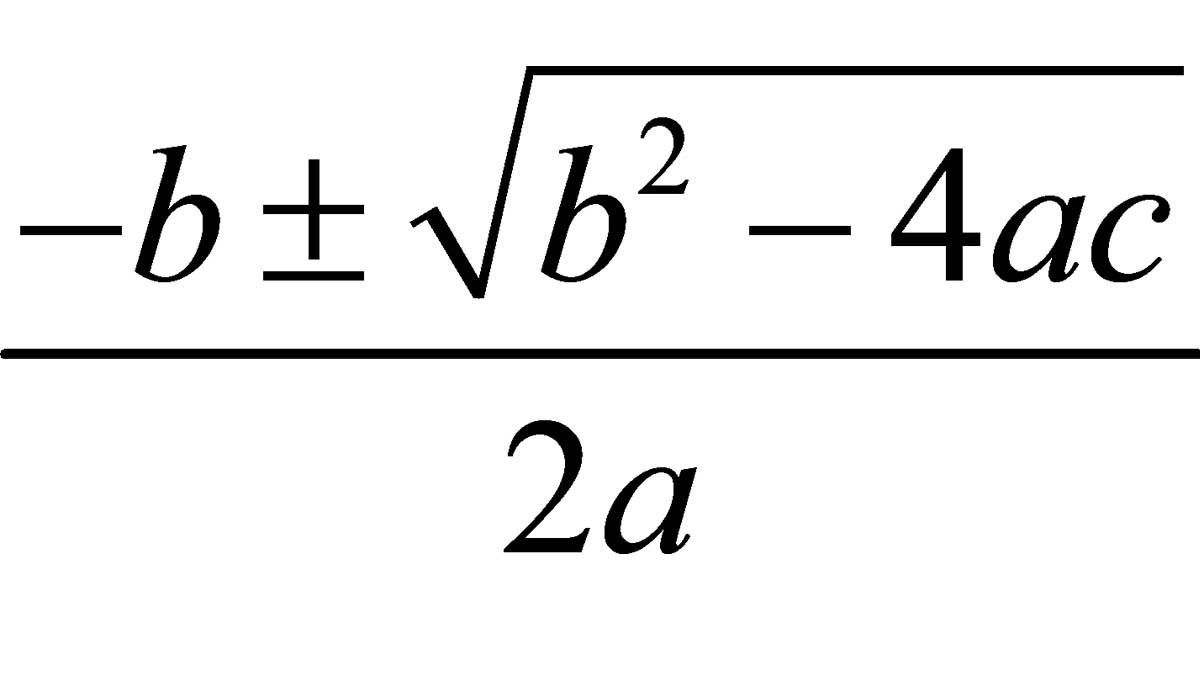
ECUACIÓN GENERAL
Ecuaciones incompletas
Sin término independiente:
Son de la forma:
ax2 + bx = 0, cuyas raíces son x1= 0; x2=-b/a.
Ecuaciones bicuadradas
Éstas son un caso particular de la ecuación de cuarto grado. Les faltan los términos a la tercera y a la primera potencias. Su forma polinómica es:
ax4 + bx2 + c = 0
Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable x2 = u
Con lo que queda: au2 + bu + c = 0. El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula anterior con x1 y x2.
Al deshacer el cambio de variable aparecen las cuatro soluciones:
- X1 = + √u1
- X2 = – √u1
- X3 = + √u2
- X4 = – √u2